OBEB – OKEK konumuz kpss matematik dersinde en sık ve neredeyse her yıl soru gelen bir konudur. OBEB – OKEK olarak kısaltılan bu konular Ortak Katların En Büyüğü ve Ortak Katların En Küçüğü anlamındadır. Önceki konumuzda Asal Çarpanlara Ayırmayı hep birlikte incelemiştik. Sıradaki konumuz ise OBEB – OKEK konusu olacak.
OBEB – OKEK
a. OBEB
Aynı anda iki veya daha fazla tam sayıyı bölen pozitif bölen sayıların en büyüğüne bu sayıların Ortak Bölenlerinin En Büyüğü (OBEB) denir. İki yolla bulunabilir.
1. Yol
Verilen sayılar birlikte asal çarpanlarına ayrılır. Bu iki sayıyı aynı anda bölebilen sayılar işaretlenir. Ve işaretlenen bu sayılar çarpılır.
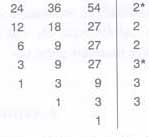
OBEB (24,36,54)=2.3=6
2. Yol
Verilen sayılar asal çarpanlara ayrılır ve ortak asal çarpanlardan üslerinin en küçük olanları alınır ve çarpılır.
24=8.3= $\displaystyle {{2}^{3}}{{.3}^{1}}$ (2 ve 3 asal)
36=4.9= $ \displaystyle {{2}^{2}}{{.3}^{2}}$ (2 ve 3 asal)
54=2.27= $ \displaystyle {{2}^{1}}{{.3}^{3}}$ (2 ve 3 asal)
Tabanları aynı olanlardan üssü en küçük olanların çarpımı;
OBEB(24, 36, 54) = 2.3 = 6 dır.
B. OKEK
İki yada daha fazla tam sayının ortak katlarının en küçüğüne OKEK denir. OKEK iki yolla bulunabilir.
1.Yol
Verilen sayılar beraber asal çarpanlara ayrılır ve bu sayıları bölen asal çarpanlar birbirleriyle çarpılır.
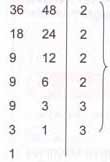
OKEK (36, 48)$ \displaystyle ={{2}^{4}}{{.3}^{2}}$
=16.9=144
2.Yol
Sayılar asal çarpanlarına ayrılır. Ve ortak asal çarpan sayılardan üslerinin en büyükleri ile ortak olmaya asal çarpan çarpılır.
$ \displaystyle 24={{2}^{3}}.3$
$\displaystyle 60={{2}^{2}}.3.5$
$ \displaystyle OKEK(24,60)={{2}^{3}}.3.5=120$
OBEB bölen sayıyı ( genellikle küçük sayıyı), OKEK ise bölünen sayıyı (genellikle büyük sayıyı) temsil eder. OBEB i ve OKEK i alınacak sayılar eşit ise OBEB ve OKEK o sayıya eşittir.
$ \displaystyle \frac{a}{x}=k$ $ \displaystyle \frac{b}{x}=t$
a=kx, b=xt olacak şekilde k ve t aralarında asal sayılar mevcuttur.
k=a, y.t=a olacak şekilde k ve t aralarında asal sayıları mevcuttur.
OKEK(x,y)=b ise
x+y nin en büyük değeri a+b olabilir.
OBEB(a,b)=1
OKEK(a,b)=a.b dir.
Kpss genel yetenek matematik dersine ait OBEB – OKEK konusu tamamlanmıştır. Bir sonraki kpss genel yetenek matematik konumuz ise Rasyonel Sayılar olacaktır.


bunlar kolay konular bana zor soru getirin arkadaş!
tmm krdşm
Ekok( 6/25, 8/15) / ebob( 6/25,8/15 ) bu sorular nası çözülüyo
ben üniversite hazırlığım 1.senem konuya detaylı çalışayım karşıma çıkarsa böyle tarz soru(sizin sorduğunuz gibi) cevaplayacağım. Şimdi Web’de aradım bulursam cevaplarım.
1 yıl olmuş atalı ama olsun.
ebob ile obeb in , ekok ile de okek in ne farkı var
farkı yok
Sen ne gadar zekisin ele
Obeb okek nasil ben anlamadim
Bu soruyu hocalarınızdan sıkça duymuşsunuzdur: ‘Neresini anlamadın’?
1-anladığım=anlamadığım
Ya bunlar çok kolay hemen yaparız ama bazen gereksiz yerde bile bölmede yanlışlık yapabiliyoruz herkese başarılar başarılar tabiki banada
Bunlarmi kolay!!!!!!
sana göre zor mu
Kardeşim büyük parçadan kücüğe doğru hareket edersen Obeb dir örneğin bidonların icine su koymak gibi kaç lt gerekli gibi tarlanın etrafına ağaç ekmek gibi bir tel i parçalarına ayırmak gibi
Kücük parçadan da büyüğe gidersen Okek tir yanı fayanslardan oda yapmak , kücük parçalardan bir tel yapmak veya bulusma soruları kac kez tur atar soruları her daim okek tir
Obeb okek sorularinda en az en fazla dedigi zaman obebi mi okeki mi almam gerekiyor. Hep karistiriyoruz. Yardimci olur musunuz?
OKEK (ortak katların en küçüğü) içinde k var küçük ten hatırla ama katlar dediği için okek obebden buyuk çıkar çinkü iki sayının buluştuğu katlardır ör:3 ile 5 in okek’i 3*5:15 te buluşurlar yani 15 i hem 3 böler hemde 5 böler
OBEB (Ortak katların en büyüğü) içinbe b var büyük 3 ile 5 in obebi ortak, bolenini bulalım = ikisinide 1 böler
Gülistan hanım sorunuzu yanlış anlamışım 🙂
en küçüğü derse okek (içinde k var küçük ten hatırla)
en buyuüğü derse obeb (içinde b var büyükten hatırla )
Cnm bnm küçük ün ilk harfi k okek te k var büyük ün ilk harfi b obeb de b çok var
Okek (24÷5,9÷10,16÷15) kaca esittir
Sonuncu olan 16/15 den dolayı bulunamaz kardeşim