Geometri dersinin ilk konusu olan nokta, doğru ve düzlem kavramlarını inceleyelim:
1) Nokta: Bir kalemin düzlem üzerinde bıraktığı ize nokta demekteyiz. Boyutu olmayan noktalar büyük harflerle gösterilir.
2) Doğru: Sonsuz noktalar kümesine doğru demekteyiz. Doğru tek boyutludur ve iki ucu sınırsızdır. Bir doğru üzerinde bulunan noktalara doğrusal noktalar denir. Farklı iki noktadan da yalnız bir doğru geçmektedir.
İki nokta arasındaki uzaklık, bu noktalara gelen gerçel sayıların farkının mutlak değeri denmektedir. Buradan çıkaracağımız şey iki nokta arasındaki uzaklık kesinlike bir negatif değer olamaz.
![]() Burada A ile B arasındaki uzaklık |AB|=|x-y| şeklinde ifade edilmektedir.
Burada A ile B arasındaki uzaklık |AB|=|x-y| şeklinde ifade edilmektedir.
* Doğru Parçası: Bir doğrunun belirlenen iki nokta arasında kalan doğrusal tüm noktalar kümesine, bu iki noktanın doğru parçası denir.
3)Düzlem: Üzerinde doğrular çizilebilen yüzeylere düzlem demekteyiz. İki boyutlu olan dğzlemin boyutları sınırsızdır. Bir noktadan sonsuz sayıda düzlem geçeceği gibi , bir nokta kümesinin tüm noktaları aynı düzlemin içindeyse bu kümenin noktaları düzlemseldir diyebiliriz. Bir noktadan sonsuz sayıda düzlem geçebileceği gibi bir doğrudan da sonsuz sayıda düzlem geçmektedir.
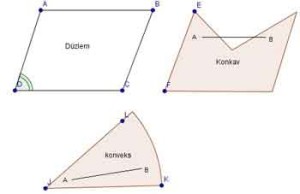
Bunların dışında, bir nokta kümesinin herhangi iki noktasını birleştiren doğrunun tamamı kümenin içindeyse buna konveks (Dış Bükey) küme, tamamı değil de bir kısmı dışında kalıyorsa konkav (iç bükey) küme denir. Aşağıdaki şekilleri kontrol edebilirsiniz.
AÇILAR
Geometri konularında karşımıza en çok çıkacak olan terim açıdır. Bir çemberi 360 eşit parçaya böldüğümüzde her bir yayın ölçüsü 1 derece olmaktadır. Ölçüleri eşit olan açılara da eş açılar denir.
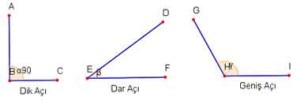
* Açı Türleri:
– Dar Açı: Ölçüsü 0 ile 90 derece arasında olan açıladır.
– Dik Açı: Ölçüsü 90 derece olan açıdır.
– Geniş Açı: Ölçüsü 90 derece ile 180 derece arasında olan açılardır.
– Doğru Açı: Ölçüsü 180 derece olan açılardır.
– Tümler Açı: Ölçüleri toplamı 90 derece olan iki açıya tümler açılar denir.
– Bütünler Açı: Ölçüleri toplamı 180 derece olan iki açıya bütünler açılar denir.
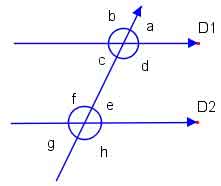
– Yöndeş Açı, Ters Açı, İç Ters Açı ve Dış Ters Açı: Bu açıların eşitlikleri aşağıda verilmiştir.
Yöndeş Açılar: a=e, b=f, c=g, d=h
Ters Açılar: a=c, b=d, e=g, f=h
İç Ters Açılar: c=e, d=f. Burada doğrular üzerine bir Z çizerseniz ya da ters bir Z çizerseniz , çizdiğiniz Z harfinin iç kısımlarında kalan açılar iç ters açıları verecektir.
Dış Ters Açılar: a=g, b=h
Görüldüğü üzere yöndeş, ters, iç ters ve dış ters açılar birbirlerine eşittir.
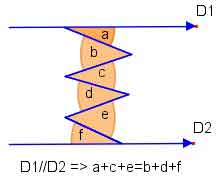
Kpss Geometri dersinin paralel açılarla ilgili son olarak aşağıdaki formülü aklımızda tutmamız iyi olacaktır.

geometri çeşitleri nelerdir bulamadım yardımcı olursanız
aradığımı bulamadım
çok kötü
Süper ßir Site
teşekkür ederim.
tam istediğim gibi teşekürler
gerçekten çok faydalı bilgileri özetlemişsiniz teşekkür ederiz…
çok güzel bir site ellerinize sağlık çok yardımcı oldunuz
tşk ler gerçekten çok güze. ellernze sağlık
tesekkurler bilgileriniz icin…
çok güzel yazı hocama verdim . hoca bana 100 verdi
ya birşey dicem neden dogru parçaskı ve ışınyok
gerçekten dersime yardımcı oldunuz çok teşekkür ederim koyu daha iyi anladım
çok teşekkürler tam istediim gibi yha 🙂
geometrinin temel konusu doğruda açılardır. o yüzden bu konuyu çok iyi yapabilmek gerekiyor.
doğru
geometri aslında anlaşılmayan bir konu benim için ama temel konuları kavrarsan çok eğlenceli. bende öğrenmeyi umuyorum inşallah başarılı olurum:D
Bende bu konuyu ariyodum Teşekkürler