Dikdörtgen konumuzda dikdörtgenin özellikleri ile eşkenar dörtgen ve özelliklerini son olarak da kare ve özelliklerini inceleyeceğiz. Dikdörtgen konusundan kpss sınavında bir çok soru gelmektedir. Önceki konumuzda Paralelkenarı işlemiştik. Sıradaki kpss geometri dersi konumuz ise Dikdörtgen olacaktır.
Dikdörtgen
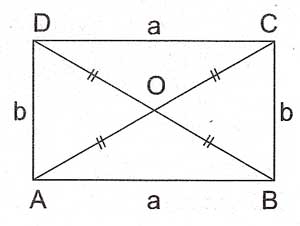
Açıları $ \displaystyle {{90}^{o}}$olan paralelkenardır. Paralelkenarın bütün özelliklerini taşıyan dikdörtgenlerin köşegenlerinin uzunlukları birbirlerine eşittir. Tüm açıları ve karşılıklı kenarları birbirine eşittir. Köşegenler birbirini ortalar.
$ \displaystyle \left| AC \right|$=$ \displaystyle \left| BD \right|$ olur.
$ \displaystyle \left| AO \right|$=$ \displaystyle \left| BO \right|$=$ \displaystyle \left| CO \right|$=$ \displaystyle \left| DO \right|$
Dikdörtgenin alanı kısa kenar ile uzun kenarın birbir ile çarpılması sonucu bulunur.
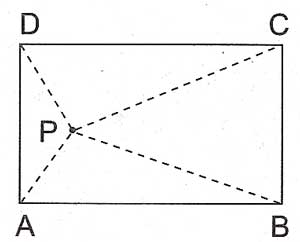
Dikdörtgenin içinde yer alan herhangi bir noktaya köşelerden çizgiler çizildiğinde, karşılıklı köşelerden çizilen 2 çizginin karelerinin toplamı diğer karşılıklı iki çizginin karelerinin toplamına eşittir.
P dikdörtgenin içinde herhangi bir nokta olsun;
$ \displaystyle {{\left| PA \right|}^{2}}+{{\left| PC \right|}^{2}}={{\left| PB \right|}^{2}}+{{\left| PD \right|}^{2}}$
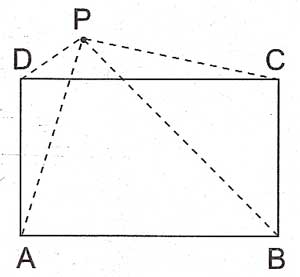
Aynı durum P noktasının dikdörtgen dışında herhangi bir noktada çizilmesi durumunda da söz konusudur.
$ \displaystyle {{\left| PA \right|}^{2}}+{{\left| PC \right|}^{2}}={{\left| PB \right|}^{2}}+{{\left| PD \right|}^{2}}$
Şimdi geometri dersinde yine karşımıza sıkça çıkan Eşkenar Dörtgen ve Kare başlıklarını inceleyelim.
Eşkenar Dörtgen
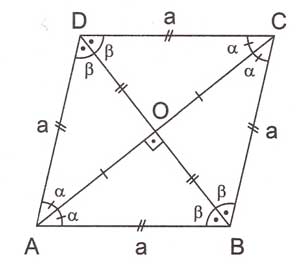
Dört kenarı eşit paralel kenarlara eşkenar dörtgen denir. Eşkenar dörtgenler paralelkenarın tüm özelliklerini taşır. Köşegenleri açıortaydır ve köşegenler arasındaki açı $ \displaystyle {{90}^{o}}$ ‘dir.
A(ABCD)= $ \displaystyle \frac{\left| AC \right|.\left| BD \right|}{2}$
Kare
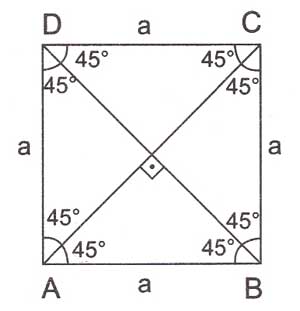
Dört kenarı eşit olan dikdörtgenlere kare denir. Paralelkenar, dikdörtgen ve eşkenar dörtgeni tüm özelliklerini taşır.
$ \displaystyle \left| AC \right|=\left| BD \right|=a\sqrt{2}$
Alan=$ \displaystyle {{a}^{2}}$ veya
Alan=$ \displaystyle \frac{{{\left| AC \right|}^{2}}}{2}$
Kpss genel yetenek geometri dersi dikdörtgen, eşkenar dörtgen ve kare konusunu tamamladık. Bir sonraki genel yetenek geometri dersi konumuz Yamuk olacaktır.


her kare eşkenar dortgenmidir
Hayır çünkü eşkenar dörtgenin köşegenleri birbirini ortalamaz fakat karede ortalar
Eşkenar dörtgendede ortalar
her kare bir eşkenardır ancak her eşkenar bir kare olmayabilir
İç açıları ne
Hiç bir şey anlamadım kafa basmı yo
bu nota göre geometri yok kardeşim tamam mı okadar parelel dikdörtgense boşuna çalışmayım ben
Elinize dünya kadar kitap alın, bu notların dışına anlatım olarak çıkamazsınız. Bu bölüm sadece anlatım kısmıdır. Sorular henüz eklenmemiştir. Saygılar.