Açı kenar bağıntıları ile ilgili Kpss son 12 yılda 5 soru çıkarmıştır. Yıllara göre soru çıkma oranı fazla olmasa da geometri sorularının kpss puan hesaplamasında belirleyici rol oynadığını bildiğimiz için üçgende açı kenar bağıntıları konusunu iyi anlamamız gerekmektedir.
Üçgende Açı Kenar Bağıntıları
- Bir üçgende herhangi bir kenarın uzunluğu , diğer iki kenarın toplamından küçük, farkının mutlak değerinden ise büyüktür. Aşağıda bu açı kenar bağıntıları ile ilgili formül yer almaktadır.
|b-c| < a < b + c
|a-c| < b < a + c
|a-b| < c < a + b
Daha iyi anlamamız açısından bir örnek verelim.
Örnek: Yukarıdaki ABC üçgenine göre |AB|=4, |AC|=8 ise |BC| uzunluğunun alabileceği değerleri nelerdir?
Çözüm: |BC| uzunluğu yani a kenarı bizden isteniyor. Yukarıdaki formüle göre:
8-4<a<8+4 => 4<a<12 sonucu çıkar. Bunun da anlamı a’nın alabileceği değerler 5,6,7,8,9,10,11 değerleridir.
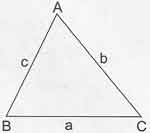
- Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.
sonucu çıkmaktadır.
- Kpss geometri üçgende açı kenar bağıntıları konusunda bir diğer önemli nokta da geniş açı ve dar açı şartlarıdır.
olmak üzere;
olmak üzere;
olmak üzere;
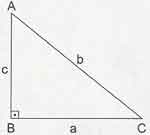
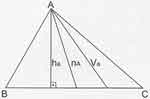
- Geometri dersinin bu konusunda bir diğer özellik de çeşitkenar üçgenle ilgilidir. Çeşitkenar bir ABC üçgeninde A köşesinden çizilen yükselik, açıortay ve kenarortay arasında bir bağıntı oluşmaktadır. Bu bağıntı şu şekildedir:
- Bir üçgenin iç açıları arasındaki sıralama ile yardımcı elemanları arasındaki sıralama terstir.
olmak üzere;
Şimdi de kpss geometri dersinin üçgende açı kenar bağıntıları konusu ile ilgili birkaç örnek çözelim.
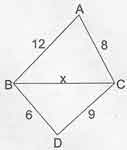 Örnek: ABCD bir dörtgen olmak üzere;
Örnek: ABCD bir dörtgen olmak üzere;
|AB|=12, |AC|=8, |BD|=6, |DC|=9 olduğuna göre |BC|= x’in alabileceği tam sayı değerleri kaç tanedir?
Çözüm: ABC üçgeninde; 12-8<x<12+8 => 4<x<20
BCD üçgeninde; 9-6<x<9+6 => 3<x<15
Bu iki üçgenin sonucunu ortak çözersek
4<x<15 olacağından x’in alabileceği değerler 10 tane olacaktır.
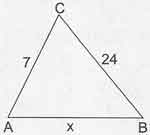 Örnek: ABC bir üçgen, |AC|=7, |CB|=24 olmak üzere;
Örnek: ABC bir üçgen, |AC|=7, |CB|=24 olmak üzere;
Yandaki şekilde C açısı geniş açı olduğuna göre |AB|=x’in alabileceği en küçük tam sayı değeri kaçtır?
Çözüm: Üçgen eşitsizliğinden;
24-7<x<24+7 burdan 17<x<31 sonucu çıkar.
Geniş açı sorulduğundan m(C)>90º olduğuna göre;
x²>7²+24²
x>25 => 25<x<31 olacağından x’in alabileceği en küçük tam sayı değeri 26 olacaktır.
Bir sonraki genel yetenek geometri dersinin konusu özel üçgenler olacaktır.

son sorunun çözümünü anlamadım. X>25 bu nasıl oluyor??
geniş açı olduğu için geniş açının karşısında büyük kenar olması gerekiyor oradaki en büyük kenarda 24 olduğundan bir büyüğü olması gerekiyor bir büyüğüdür 25 ondan
hic bisey anlamadm cok karisik
peki iki kenarı bulmaya calısırken napcazz.
Hic bisy anlamadim:((((
güzedi beğendim
150 soru acı kenar bagıntısı lazım lutfen yardım edın
bu konu 9.sınıf mı?
sağolun yararı büyük
çok iyi bir site ödevlere çok yardımcı
teşekkürler süper olmuş
bence çokk iyiiii
teşekkürler 😀 çok yardımcı oldunuz 😀
süper anlatmışlar çook teşekkür ederim
çözemediğim bir geometri sorusu var.kime sorabilirim? dosya ekleme seçeneği olmadığı için sitenin eposta adresi verir misiniz?
ya biraz karışık ama ii bence 🙂
çok karışık biraz daha düzgün yazsanız
Çok teşekkür ederim harikasınız!
hiç biryerde dar açılı ve geniş açılı üçgeni bulamadım 🙁
Dar açılı üçgen ya da geniş açılı üçgenle ilgili açı-kenar bağıntılarını arıyorsanız konu içinde mevcuttur. Eğer dar açılı ve geniş açılı üçgen tanımını istiyorsanız;
Dar Açılı Üçgen: Bir üçgende açıların hepsi 90 dereceden küçükse o üçgene dar açılı üçgen denir.
Geniş Açılı Üçgen: Bir üçgende herhangi bir açı 90 derecen büyükse o üçgene de geniş açılı üçgen denir.
başka sitelere bak…
bence güzel ben begendim arkadaşlar hepsi güzel zekice düşünürsek süper tavsiye ederim amasizi bilemem malesef canım
çok güzel birv site tuum ödevim bitti