Üçgende Benzerlik

PAYLAŞ

Üçgende benzerlik konusu kpss geometri dersi dahilindedir. Bilindiği üzere kamu personeli seçme sınavında genel yetenek bölümünde geometri ile ilgili az soru çıkmaktadır. Buna paralel olarak da üçgende benzerlik konusuyla ilgili son 12 yılda sadece 2 soru çıkmıştır. Ancak yüksek puan hedefleyen memur adaylarının bu konuyu iyi kavraması gerekmektedir. Üçgende benzerlik konusu içinde mantığı da barındırdığı için diğer geometri konularına göre daha zevklidir.

Üçgende Benzerlik

Kpss geometri konusunda, bir cismin belli bir oranda büyütülmesi ve küçültülmesi ile oluşan şekiller birbirlerinin benzeri olarak adlandırılır.

Bütün çemberler ve bütün kareler benzerdir.

Her üçgen benzer değildir. Üçgenlerin benzer olabilmesi için, iki üçgen arasında yapılan karşılaştırmada bu iki üçgenin iki iç açısı eşit veya bu üçgenlerin kenarlarının orantılı olması gerekmektedir. Eğer bu şartlar gerçekleşirse bu iki üçgen benzer üçgendir denir.

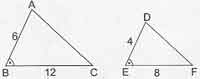
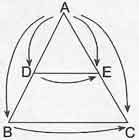
Yandaki ABC üçgeni ile DFE üçgeni benzer üçgenlerdir. Bu benzer üçgenler $ABC \sim DFE$ şeklinde gösterilir. Ayrıca bu iki benzer üçgen arasındaki bağıntılar da şu şekildedir:

$m(\hat A) = m(\hat D)$ , $m(\hat B) = m(\hat F)$ , $m(\hat C) = m(\hat E)$

$\frac{{|AB|}}{{|DF|}} = \frac{{|BC|}}{{|FE|}} = \frac{{|AC|}}{{|DE|}} = k$

Buradaki ”k” benzerlik sabitidir. Eğer ”k” 1 ise üçgenler eşittir denir.

İki üçgen arasında bulunan benzerlik oranı bu iki üçgenin çevreleri, yükseklikleri, açıortayları ve kenarortayları arasında da bulunur. Yani iki üçgen arasında benzerlik oranı 2 ise yükseklikleri oranı da 2 olacaktır. (Yükseklikleri çizilen kenarların oranı aynı olmalıdır.)

Kpss geometri üçgende benzerlik konusunda, İki üçgen arasında bulunan benzerlik oranının karesi bu iki üçgenin alanları oranına eşittir.

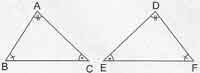
Açı – Açı Benzerliği: Herhangi iki üçgenin iki iç açısı eşit ise bu üçgenler benzer üçgenlerdir.

Buradan zaten iki iç açısı eşitse üçüncü açı da eşittir anlamı çıkmaktadır.

Açı – açı benzerlik teoremini bir örnekle açıklayalım.

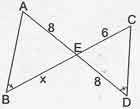
ABE ve ECD birer üçgen olmak üzere; $m(\hat B) = m(\hat D)$

$[AD] \cap [BC] = E$

$|AE| = |ED| = 8$

$|EC| = 6cm$ ise $|EB| = x$ kaç cm’dir?

$m(A\hat EB) = m(C\hat ED)$ ters açı olduğundan üçüncü açı olan $m(B\hat AE) = m(E\hat CD)$ açıları eşit olur. Buradan $ABE \sim CDE$ benzerliği ortaya çıkmaktadır. Dolayısıyla benzerlik bağıntısını belirtirsek sonuca ulaşmış oluruz. $\frac{6}{8} = \frac{8}{x} = > x = \frac{{32}}{3}cm$

Kenar Açı Kenar Benzerliği: Üçgende benzerlik konusu içindeki kenar açı kenar benzerliği, iki üçgenin birer açıları eşit ve bu açıları oluşturan kenarlar orantılı olduğu zaman oluşmaktadır.

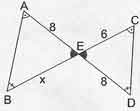
Yandaki benzer iki üçgende ortak açıları oluşturan kenarları orantıladığımızda şu eşitliği elde ederiz: $\frac{4}{8} = \frac{6}{{12}}$

Kenar – Kenar – Kenar Benzerliği: Bu benzerlikte de iki üçgenin tüm kenarları orantılı ise üçgenlerde benzerlik ortaya çıkar.

Kenar kenar kenar benzerliğinde orantılı kenarları gören açıların ölçüleri de eşittir.

Temel Benzerlik Teoremi: Orantılı doğru parçaları ya da Thales olarak da adnlandırılan temel benzerlik teoremi şu şekilde olmaktadır.

$\frac{{|AD|}}{{|AB|}} = \frac{{|AE|}}{{|AC|}} = \frac{{|DE|}}{{|BC|}}$ Ayrıca bu şekilde oluşan temel benzerlik teoreminde $[DE]//[CD]$ paralelliği de ortaya çıkmaktadır.